输入两个链表,找出它们的第一个公共节点。
如下面的两个链表:
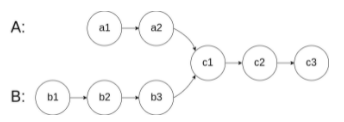 |
在节点 c1 开始相交。
示例 1:
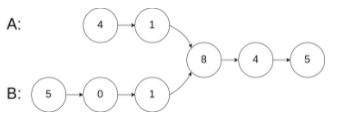 |
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
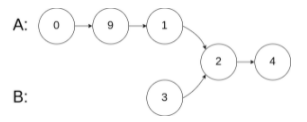 |
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
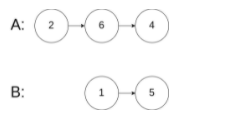 |
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
思想主要采用一个堆栈(先进后出)的性质,将链表节点入栈,进而的去判断,看是否 节点的地址指针是否是相同的
| /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: /* 先采用链表反转,然后从后往前依次的做比较 如果两个链表没有交点,返回 null. 在返回结果后,两个链表仍须保持原有的结构。 可假定整个链表结构中没有循环。 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。 */ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) { if(!headA || !headB) return nullptr; stack<ListNode*>a,b; ListNode* tep; tep = headA; while(tep){ a.push(tep); tep = tep->next; } tep = headB; while(tep){ b.push(tep); tep = tep->next; } if(a.top() != b.top()) return nullptr; while(!a.empty() && !b.empty()){ tep = a.top(); ListNode* t1 = a.top(); a.pop(); ListNode* t2 = b.top(); b.pop(); // 首先有两种情况需要判定一下 当 弹出后,可能存在 a,b 栈为空的情况下,这时候 判定, 若两个栈都不为空的情况下 printf 即可 if(t1 == t2 && (a.empty() || b.empty())) return t1; if(t1 == t2 && !a.empty() && !b.empty() && a.top() != b.top()) return t1; } return nullptr; } // ListNode *reverseL(ListNode* head){ // if(!head || !head->next) return head; // ListNode* a = head; // ListNode* b = NULL; // ListNode* p = head; // while(p){ // a = p; // p = p->next; // a->next = b; // b = a; // } // return a; // } }; |